28.04.2020
Temat: Interpretacja geometryczna i fizyczna pochodnej.
- Zapoznajemy się z interpretacją geometryczną pochodnej i sporządzamy notatkę (wraz z wykresem):
Interpretacja geometryczna pochodnej Pochodna funkcji f(x) w punkcie x0 – to współczynnik kierunkowy prostej stycznej do f(x) w punkcie x0.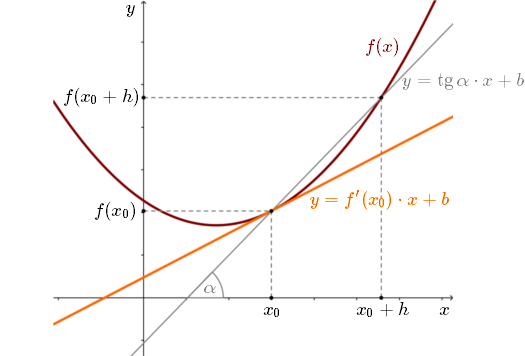
Zauważmy, że jeśli h→0, to szara prosta zbiega do pomarańczowej prostej.
Możemy wręcz napisać, że:
Pochodna pokazuje nam jak funkcja zmienia się w danym punkcie. Dokładniej:
- Jeśli f′(x0)>0, to funkcja f(x) rośnie w punkcie x0.
- Jeśli f′(x0)=0, to funkcja f(x) jest stała w punkcie x0.
- Jeśli f′(x0)<0, to funkcja f(x) maleje w punkcie x0.
2. Zapoznajemy się z interpretacją fizyczną pochodnej i podobnie robimy notatkę :
• Równanie prostej stycznej do wykresu funkcji f różniczkowalnej w punkcie
x0:
y − f(x0) = f'(x0)(x − x0).
• Pochodna wyraża szybkość przyrostu funkcji w chwili x0.
• Jeśli s = s(t), jest funkcją drogi w zależności od czasu, to pochodna s'(t0) jest prędkością w chwili t0.
• Jeśli v = v(t), jest funkcją prędkości w zależności od czasu, to v'(t0) jest
przyśpieszeniem w chwili t0.
3. Po sporządzeniu notatki zapoznajemy się z filmem:
Potwierdzeniem Waszej dzisiejszej aktywności jest odpowiedź na pytanie ile wykresów należało dzisiaj narysować? proszę o odpowiedź do godziny 15.00. KOnsultacje 8.45-9.00. Pozdrawiam I.Sokołowska
