28.04.2020
Temat1: Proporcjonalność odwrotna.
Zapoznajemy się z materiałem:
PROPORCJONALNOŚĆ OWDROTNA
Zagadnienia: matematyka – podstawówka, gimnazjum – proporcjonalność odwrotna, wielkości odwrotnie proporcjonalne
Mamy z nią do czynienia, gdy wielkości są odwrotnie proporcjonalne, to znaczy, że łączy je zależności powodująca, że wraz ze wzrostem jednej wartości, druga maleje tyle samo razy. Działa to też w drugą stronę: gdy pierwsza wielkość maleje, to druga rośnie tyle samo razy.
Przykład:
Aby wykonać pewną pracę w ciągu 10 godzin, potrzeba 2 pracowników. Ilu pracowników potrzeba, aby wykonać tą pracę w ciągu 4 godzin?
Powyższe wielkości: liczba pracowników i liczba godzin – są odwrotnie proporcjonalne. Im więcej pracowników wykonuje daną pracę, tym mniejszą liczbę godzin zajmie im jej wykonanie. Ile razy więcej pracowników, tyle samo razy mniej godzin będą potrzebować.
Aby ustalić, że dwie wartości są odwrotnie proporcjonalne, możemy wspomóc się zapisem proporcji. W tym celu zapisujemy obok siebie odpowiadające sobie wartości, przy czym wartość nieznaną zapisujemy jako x. (10 godzin odpowiada 2 pracownikom, 4 godziny odpowiadają x pracownikom):
Po zapisaniu proporcji, zapisujemy działanie zgodnie z zasadą:
– liczbę znajdującą się w tej samej linii co x – pod kreską ułamkową,
– pozostałe liczby, przemnożone przez siebie – nad kreską ułamkową.
Odpowiedź: Aby wykonać daną pracę w ciągu 4 godzin, potrzeba 5 pracowników.
Narysuj zależność dwóch wielkości odwrotnie proporcjonalnych opisanych równaniem:
Przekształcamy wzór dzieląc go stronami przez x:
Dla tak otrzymanego wzoru funkcji wyznaczamy kilka punktów należących do wykresu:
| x | 0,2 | 0,5 | 1 | 2 | 4 |
| y=1x | 5 | 2 | 1 | 0,5 | 0,25 |
Następnie rysujemy wykres: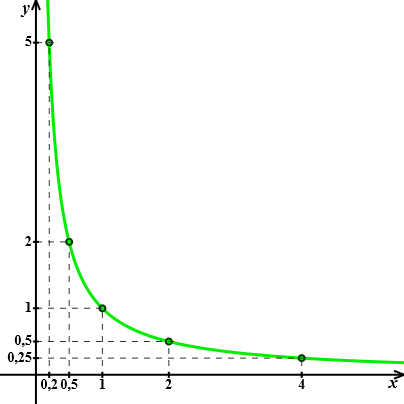
Wykres narysowaliśmy tylko dla x>0.